Hadoop - Architecture

I started learning about distributed file system. It is based on Google File Systems. It is targeted for data intensive applications. It is scalable and fault tolerant. It is targeted to run on cheap commodity computers which are bound to fail either the whole machine crashes or its disk experience intermittent failures. Also when we are connecting large set of computers, some computers may gets disconnected due to network failures. So in normal file systems failure is just exception cases, but in Google file system and Hadoop it is a norm. That is these file systems are designed with failure as certainties.  

Obviously your question would be what is the usual number of computers present within this distributed environment? Hmmm I guess numbers in 1000s. These can be present in same data centers or  it might be present in different data centers all together. 

Next question would be what are we going to process in these system of computers? If we are having this much computers should be super complex computations like rocket science, weather forecast, etc. Well you can use for that as well but even simple problems need big set of machines. Let me give you an example. You have a simple text file containing some text, let us assume, its size is some 16kb. Now you write a C program to count the words occurrence in that file. How much time it takes to execute it? Well hardly seconds. Now let me give you a file with size 16 MB, still it will complete in seconds. Now if I increase it to 16 GB file, well it might drag to minutes. What if it is 16 TB? now it might run for hours before completing. How nice it would be if I can some how use parallelism in counting the words. With our normal C program also you can do that, but overhead of synchronization will lot of time to program and also with synchronization comes the deadlocks and other monsters. And what kind of synchronization are you really looking here - thread or process. Both within same machine. 

Now enters Hadoop. Hadoop provides this distributed environment of handling huge files which helps you to concentrate on the logic of the program rather than on worrying about how to make the program work. Hadoop combined with Map Reduce will help to write a simple program[ or programs] to do the word count on files which are of really huge files. Let me remind you, word counting is a simple program, suppose you want to implement a web crawler or natural language processing algorithm or some complex image processing algorithms. That time you will really utilize Hadoops distributed environment. Best thing is they are saying take a bunch of normal linux cheap machines combine them and you get a beast out of it.

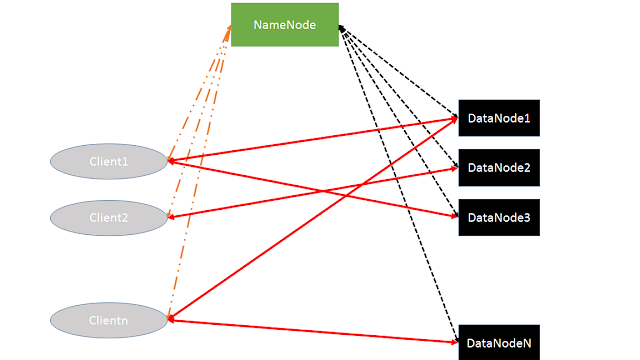
Hadoop is a client server model. There is a Master [namenode], a set of sub masters [datanode] and then there are clients. There is a lot of theory why we need to go to this architecture and what benefits we are gaining by using this architecture. Also why each component has to handle responsibilities in a particular way? I would recommend to read Google File System paper to understand it. In a future post, I will go through GFS. 

In Hadoop, given a file, that file is divided into fixed sized blocks. Usually it will be 64 MB blocks. So client will ask the namenode to add the file to HDFS(hadoop file system). Namenode will divide the file into many blocks and ask the datanodes to store those blocks in them. Now each block will be copied/replicated to 3 different datanodes. This is one of the way of making it more reliable. So a single file might be spread across multiple datanodes. The number of replication can be configured.

So namenode will track the files namespace and also file mapping that is File to blocks mapping. Then where exactly those blocks exists?  that is in which data nodes does the block exists. All this information is kept in memory. Now obviously if namenode fails everything is lost right? And what was the need to keep in memory? Well it is fast. To avoid loosing the data there is a method. There is a base image of hadoop - Fsimage and then there is log file EditLog. Each time a modification happens to the file system like addition of new file, deletion of files, changes to files an entry will be made in the EditLog. So incase of namenode failures, when namenode is restarting, it will use the FsImage as base and start the file system, then it will read the EditLog and starts making changes to that filesystem. Once everything is updated, it will write those changes to FsImage and truncates the EditLog so that fresh changes can be written to the EditLog. 

So the datanodes actually has data. Each of these blocks are stored in the form of local files. So to do any read or write to the files blocks client will ask the namenode to whom should it contact. Namenode will give the list of datanodes. Client will then contact the datanodes to do actual data transfer. By doing this we are reducing the network traffic to namenode. Namenode keeps track of datanodes by means of heartbeats. That is every now and then, datanodes will send a message to namenode giving the report like how many blocks it has, if there is any disk failures, etc. Suppose namenode did not receive a message from datanode for a while, namenode assumes that datanode has crashed and starts replicating the data present in that datanode to another datanode. 

I would recommend to go through this link http://hadoop.apache.org/docs/current/hadoop-project-dist/hadoop-hdfs/HdfsDesign.html#Introduction to know more about the architecture of hadoop. 

Now you might think I need atleast 3 machines - a client machine, a namenode macine and a datanode machine. But we can configure a single machine which has both datanode and namenode. And we can run our client applications run on the same machine. 

Well trying to install hadoop in a single machine. Will update the screenshot once done. Currently facing some problems.

In future, will go through Map-Reduce, Google File System, Project Voldemort and Amazons Dynamo.

Heap Sort

This sorting algorithm has 3 main parts.

1. Build Heap
2. Swap 1st element and last element, Decrease Size by 1
3. Heapify

you might be wondering now what the hell is heap?!!! Heap is a binary tree representation in which parent element will always have either highest or lowest element among its children - left child and right child. This binary tree will be represented in the array. If parent is holding highest element it is Max heap, else if parent is holding smallest element then it is Min heap. 

Below is the image of the Heap representation in tree form and also in array. 

As you can see in the tree, its a Max heap that is all the parents are having highest value when compared to (root, Left and Right). So to convert it into array - First element will be the root, followed by its immediate left child and then its immediate right child, followed by left child's children and then right child's children.

So if you have a parent index, say i, then its left child is at 2*i + 1, similarly its right child is present at 2*i+2. Similarly given an index j, the parent is present at location i/2.

First step, given an array we need to transform it into heap structure. Below is the code for doing it.

int BuildMaxHeap(int* pIntArray, int nSize)

{

int nReturnValue = 0;

if (pIntArray == 0)

{

return ERR_NULLINPUTARRAY;

}

if (nSize <= 0)

{

return ERR_INVALIDARRAYSIZE;

}

for (int i = nSize / 2; i >= 0; i--)

{

MaxHeapify(pIntArray, nSize, i);

}

return nReturnValue;

}

We start from the last parents that is parents just before leaves and check if it is satisfying Max Heap property. If not then we max heapify it. So once it is heapified we will move to next parent and repeat the procedure until root. 

int MaxHeapify(int* pIntArray, int nSize, int nIndex)

{

int nReturnValue = 0;

int nLeftIndex = LeftChildHeap(nIndex);

int nRightIndex = RightChildHeap(nIndex);

int nLargestIndex = nIndex;

int nTemp = 0;

if (nLeftIndex < nSize && pIntArray[nLeftIndex] > pIntArray[nLargestIndex])

{

nLargestIndex = nLeftIndex;

}

if (nRightIndex < nSize && pIntArray[nRightIndex] > pIntArray[nLargestIndex])

{

nLargestIndex = nRightIndex;

}

if (nLargestIndex != nIndex)

{

nTemp = pIntArray[nLargestIndex];

pIntArray[nLargestIndex] = pIntArray[nIndex];

pIntArray[nIndex] = nTemp;

MaxHeapify(pIntArray, nSize, nLargestIndex);

}

return nReturnValue;

}

So now what is this max heapify? - This will check among Parent, Left Child and Right Child which is largest element. Largest element will be swapped with Parent. Suppose left child had largest, then Parent and left elements are swapped. Once swapped we do max heapify to the exchanged element. That is, in our case if left element was exchanged with Parent, then now max heapify the new left childs children by treating it as root.

So once you are done with this you are now having the heapified array. So by max heapify theory root (0th element in array) should have the highest element among all the elements in the array/heap. To get the sorted array, Take the 0th element and swap with last element of the array. Then decrease the size of the array by one. Now heapify the array from the root. When you do this next highest element will come to the root of the heap. Repeat the process until size becomes 1. 

int HeapSortIntegers(int* pIntArray, int nSize)

{

int nReturnValue = 0;

int nTemp = 0;

if (pIntArray == 0)

{

return ERR_NULLINPUTARRAY;

}

if (nSize <= 0)

{

return ERR_INVALIDARRAYSIZE;

}

BuildMaxHeap(pIntArray, nSize);

for (int i = nSize - 1, j = 1; i >= 1; i++, j++)

{

nTemp = pIntArray[0];

pIntArray[0] = pIntArray[i];

pIntArray[i] = nTemp;

MaxHeapify(pIntArray, nSize - j, 0);

}

return nReturnValue;

}

This looks so completed right? Does it have any benefit? Well, yes its runtime is O(nlogn). Its average case = worst case runtime and it sorts inplace. 

Wow then this should be better than quicksort as quicksort takes O(n^2) in its worst case scenario? 

Well yes and no. Yes because heapsort is always O(nlogn). No because given an array, for which quick sort runs in O(nlogn), if we execute for heap as well as quick sorts, then quick will be running better as heap sort has higher constants in its runtime 

Again code is present in https://github.com/harsha-kadekar/LibraryOfAlgorithms

Implementation is based on Chapter 6 - HeapSort of Introduction to Algorithms 3rd Edition [Thomas H Cormen, Charles E Leiserson, Ronald L Rivest, Clifford Stein]

Quick Sort

This algorithm is quite tricky in terms of flow or concept. Again this algorithm is based on divide and conquer technique. In case of merge sort, importance is given to combining the divided list of elements where as dividing was very simple. But in case of quick sort, its opposite. Here importance is in dividing and there is no work for combining elements. In every iteration we try to find an element and its correct position such that all the elements are present before that element are less than that element and all the elements which are present after that element are having value greater than element. Well you may say thats the concept of ascending order, yeah true but in the first iteration only this element is brought to correct position. All those elements who are at its right are still not in their correct positions, similarly all the elements to its left. Position of this element forms the partition point. Once I get this index, I will re run my quick sort algorithm from lowest position to index - 1. Similarly from index + 1 till highest position. 

Well now we know some idea of quick sort, so what is its complexity? 

Hmmm its O(n^2). 

What?? then why we need this? We could have gone with Merge sort only right? 

Well first thing, this algorithm sorts inplace, where as merge sort needs extra space remember... Also average runtime is theta(nlogn). It is better than merge sort in most cases. 

Oh! then when does the worst case occur for quick sort?

When array is already sorted. But we can use random picking of pivot. Before starting of the pivot finding we choose a random index between low and high and then swap that element with highest index element. This kind of forces it to run in average case runtime.

Hmmm good now lets see the code.

So initial case is generating the recursive function which keeps on calling itself until all the elements are sorted.

int RandomizedQuickSort(int* pIntArray, int nlow, int nhigh)
{
int nReturnValue = 0;
int nKey = -1;

if (nlow < nhigh)
{
nKey = RandomizedPartition(pIntArray, nlow, nhigh);
RandomizedQuickSort(pIntArray, nlow, nKey - 1);
RandomizedQuickSort(pIntArray, nKey + 1, nhigh);
}

return nReturnValue;
}

To force the algorithm to run in average time, we need to randomize the pivot selection. So here is the code of RandomizedPartition which will randomly select an index and swaps its element with highest indexed element.

int RandomizedPartition(int* pIntArray, int nlow, int nhigh)
{
int nReturnValue = 0;

int nDiff = nhigh - nlow;
int nTemp = 0;

srand(time(0));

nDiff = rand() % nDiff;

nTemp = pIntArray[nhigh];
pIntArray[nhigh] = pIntArray[nlow + nDiff];
pIntArray[nlow + nDiff] = nTemp;

nReturnValue = PartitionQuickSort(pIntArray, nlow, nhigh);

return nReturnValue;
}

Finally, here is the quick sort. 

int PartitionQuickSort(int* pIntArray, int nlow, int nhigh)
{
int nCompareElement = pIntArray[nhigh];
int nTemp = 0;
int i = nlow - 1;

for (int j = nlow; j < nhigh; j++)
{
if (pIntArray[j] <= nCompareElement)
{
i++;
nTemp = pIntArray[i];
pIntArray[i] = pIntArray[j];
pIntArray[j] = pIntArray[i];
}
}

nTemp = pIntArray[i + 1];
pIntArray[i + 1] = pIntArray[nhigh];
pIntArray[nhigh] = nTemp;

return i + 1;
}

Basically I am trying to find the position of the last element in the given array. Aim is to find the position such that all elements which are less than that element should be before that position and all the elements which are greater that element should be after that position. Order of such elements is not a concern. So how do I find the correct position? I have two indices 'i' and 'j'. Index j is for iteration, i for position swapping. Each element starting from lowest index will be compared with the highest index element. If element is greater then just go ahead with doing anything. If smaller, than increase the index i, swap the elements of index i and j. Basically you are pushing the greater elements to other side. Go on doing this until j reaches highest - 1. Now i + 1 position is the correct position for the highest index element. So swap this element with element in i + 1 index. Finally i + 1 is your pivot.

Actually complete implementation is present here, but still this can be found in my github - https://github.com/harsha-kadekar/LibraryOfAlgorithms . Also implementation is based on the Chapter 7 - QuickSort of Introduction to Algorithms 3rd Edition [Thomas H Cormen, Charles E Leiserson, Ronald L Rivest, Clifford Stein]

Indian Civilization

Michel Danino's lecture series of Indian Civilization. This is a must for Indians. It gives facts and figures of how and what is Indian civilization.

https://www.youtube.com/playlist?list=PL1tPjaS1KFVVaE2LLviORsxUs31e0J_r2

Name Value Dictionary

As I was developing the basic web server, I found the need for a key value or name value dictionary to store the name value pairs. Earlier as part of my MS course curriculum I had written a chained and open addressing hash tables in python. I followed the similar pattern. Along with that "The C programming Langauage" by Brian W. Kernighan and Dennis M. Ritchie book in section 6.6 also explains about creating the name value list.

I have created a chained hash table. One of the main feature of hash table or dictionary is searching or retrieving of the stored value is fast. It should be O(1). If I had used Open addressing table than I could have achieved this. But with chained hash table we are heavily dependent on the hash function. So there may be chances that search will take more than O(1). 

Okay let me first explain the dictionary function. Suppose you have key value pairs like 'employee name' and 'employee id' or 'programming languages' and 'C, C++, javascript, C#', etc. Now I need a data structure to store such key value pairs. I should be able to keep on adding and updating such key value pairs without worrying about where they get stored and memory limit. For an external user it is an infinite memory bucket, where he/she keeps on dumping key:value pairs. User can add new key:value pair, access the already stored key:value pair, update value of existing key:value pair, search for a key.

Now let me explain the implementation details. Initially when I am creating the dictionary a default sized array will be created where all name value pairs will be stored. As the array gets filled up, we try to increase the array size and rebuild the dictionary. This, we will try to do by monitoring the load factor. Example if the load factor = (Number of current nodes/Size of Dictionary Array) is greater than 0.8 then we increase the Array size and rebuild the dictionary array. You may wonder why dictionary has to be rebuilt. See our hash function which gives the index of the array, where the name value needs to be stored will use the size of the array to generate the index. So when array size changed then for the same old key, hash value will give you some other index. So literary you lost all the old nodes of dictionary. To avoid this error, once new array is created, all the old values has to be re added/hashed to this new array.

Given a key, we will pass that key to a hash function. This hash function will give you an integer which will be within 0 and array size of dictionary. This will be index in the array where we will be saving the name value pair. There are chances of collision that is two keys can lead to generation of same index. In this scenario there are many ways to handle it. we are using chained hashing. Here each entry in the array is a singly linked list. Each node in the singly linked list, represent  the name value pair. So if in an index already another name value pair is present then we will be adding to this list new name value pair. 

So when given a key, First step is to get the index using the hash function. Using this index we can get the singly list of all the keys which are having same index. Now traverse the singly list to find the exact key value pair.

This is my dictionary node. A dictionary node has a key (strName) and a value (strValue). As this node will be part of the singly linked list, we have self referencing pointer 'next'

typedef struct structDictionaryNode
{
 char* strName;
 char* strValue;
 struct structDictionaryNode* next;
}DictionaryNode;

This is my actual dictionary. LoadFactor will define when I need to rebuild by dictionary by increasing the size of buffer array. nSizeOfDictionary is the size of the buffer array that is total slots available for allocation. nCurrentSize will tell you how many key value pairs are currently present in the dictionary. So current load factor can be calculated by nCurrentSize/nSizeOfDictionary. dictionaryArray will be my buffer array, basically it is array of singly linked lists.

typedef struct
{
 float LoadFactor;
 int nSizeOfDictionary;
 int nCurrentSize;
 DictionaryNode** dictionaryArray;
}Dictionary;

This function is used to create the dictionary. As you can see we are using load factor as 0.8. Also size of the initial array is passed.

Dictionary* CreateDictionary(int nSizeOfDictory)
{
 Dictionary *dict = 0;
 int i = 0;

 if (nSizeOfDictory == 0)
  nSizeOfDictory = 10;

 dict = (Dictionary*)malloc(sizeof(Dictionary) * 1);
 if (dict == 0)
 {
  //Error handle it
  return dict;
 }

 (*dict).LoadFactor = 0.8;
 (*dict).nSizeOfDictionary = nSizeOfDictory;
 (*dict).nCurrentSize = 0;
 (*dict).dictionaryArray = (DictionaryNode**)malloc(sizeof(DictionaryNode*)*(*dict).nSizeOfDictionary);

 for (int i = 0; i < (*dict).nSizeOfDictionary; i++)
  (*dict).dictionaryArray[i] = 0;


 return dict;
}

This is the hash function used to find the actual index where the node needs to be placed in the dictionary array.

unsigned hash(int nSizeOfTable, char *s)
{
 unsigned hashval;
 for (hashval = 0; *s != '\0'; s++)
  hashval = *s + 31 * hashval;
 return hashval % nSizeOfTable;
}

Every time you want to add a name value pair, we use below function. Also you can see, as we add a key we will verify if this addition has resulted in exceeding the load factor. If so then we are rebuilding the dictionary. If loadfactor is exceeded, then we are creating new dictionary with double the previous size.

int AddNameValueToDictionary(Dictionary *dict, char *strKey, char *strValue)
{
 int nReturnValue = 0;
 DictionaryNode *pHead = 0, *pCurrent = 0;
 int i = 0;
 float fTemp = 0.0;
 int bFoundKey = 0;

 if (dict == 0 || strKey == 0 || strValue == 0)
 {
  nReturnValue = ERR_INVALID_PARAMETERS_DICT;
  return nReturnValue;
 }

 if (IsKeyExistsInDictionary(dict, strKey) == 1)
 {
  pHead = (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)];
  if (pHead == 0)
  {
   //Actually Error
   (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)] = CreateADictionaryNode(strKey, strValue);
   (*dict).nCurrentSize++;

  }
  else
  {
   while (pHead != 0)
   {
    if (strcmp((*pHead).strName, strKey) == 0)
    {
     //Update Value
     free((*pHead).strValue);
     (*pHead).strValue = (char*)malloc(sizeof(char)*strnlen_s(strValue, MAXVALUESIZE) + 1);
     memset((*pHead).strValue, '\0', strnlen_s(strValue, MAXVALUESIZE) + 1);

     i = 0;
     while (strValue[i] != '\0')
     {
      (*pHead).strValue[i] = strValue[i];
      i++;
     }

     bFoundKey = 1;
     break;
    }
    else
    {
     pHead = (*pHead).next;
    }
   }

   if (bFoundKey == 0)
   {
    //Actually Error
    pHead = (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)];
    pCurrent = CreateADictionaryNode(strKey, strValue);
    (*pCurrent).next = pHead;
    (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)] = pCurrent;
    (*dict).nCurrentSize++;

   }
  }



 }
 else
 {
  pHead = (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)];

  if (pHead == 0)
  {
   (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)] = CreateADictionaryNode(strKey, strValue);
   (*dict).nCurrentSize++;
  }
  else
  {
   pCurrent = CreateADictionaryNode(strKey, strValue);
   (*pCurrent).next = pHead;
   (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)] = pCurrent;
   (*dict).nCurrentSize++;
   
  }

 }

 fTemp = (*dict).nCurrentSize;
 fTemp = fTemp / (*dict).nSizeOfDictionary;


 if (fTemp > (*dict).LoadFactor)
 {
  nReturnValue = RebuildDictionary(dict, (*dict).nSizeOfDictionary * 2);
 }

 return nReturnValue;
}

It is common in dictionary operations to know if a key is already present in the dictionary. Following function will return 1 if key is found in dictionary, else 0.

int IsKeyExistsInDictionary(Dictionary *dict, char *strKey)
{
 int bFound = 0;
 int i = 0;
 DictionaryNode *pHead = 0, *pCurrent = 0;

 for (i = 0; i < (*dict).nSizeOfDictionary; i++)
 {
  pHead = (*dict).dictionaryArray[i];
  if (pHead != 0)
  {
   pCurrent = pHead;
   while (pCurrent != 0)
   {
    if (strcmp(strKey, (*pCurrent).strName) == 0)
    {
     bFound = 1;
     break;
    }

    pCurrent = (*pCurrent).next;
   }
  }
 }

 return bFound;
}

This function rebuilds the dictionary with the new size.

int RebuildDictionary(Dictionary *dict, int nNewSize)
{
 int nReturnValue = 0;
 int i = 0;
 int nOldSize = 0;
 DictionaryNode *pHead = 0, *pCurrent = 0;

 DictionaryNode** pNewArray = (DictionaryNode**)malloc(sizeof(DictionaryNode*)*nNewSize);
 DictionaryNode** pOldArray = (*dict).dictionaryArray;
 nOldSize = (*dict).nSizeOfDictionary;
 (*dict).nSizeOfDictionary = nNewSize;
 (*dict).dictionaryArray = pNewArray;
 (*dict).nCurrentSize = 0;

 for (i = 0; i < nOldSize; i++)
 {
  pHead = pOldArray[i];

  while (pHead != 0)
  {
   pCurrent = pHead;
   pHead = (*pCurrent).next;

   (*pCurrent).next = 0;
   nReturnValue = AddNodeToDictionary(dict, pCurrent);
   if (nReturnValue != 0)
   {
    //Error handle it
   }
   
  }
 }

 free(pOldArray);
 pOldArray = 0;

 return nReturnValue;
}


This function will delete a particular node or name value pair from the dictionary. 

int DeleteKeyFromDictionary(Dictionary *dict, char *strKey)
{
 int nReturnValue = 0;

 int i = 0;

 DictionaryNode *pHead = 0, *pCurrent = 0, *pPrev = 0;

 pHead = (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)];
 if (pHead != 0)
 {
  pCurrent = pHead;
  while (pCurrent != 0)
  {
   if (strcmp((*pCurrent).strName, strKey) == 0)
   {
    if (pPrev == 0)
    {
     (*dict).dictionaryArray[hash((*dict).nSizeOfDictionary, strKey)] = (*pCurrent).next;

    }
    else
    {
     (*pPrev).next = (*pCurrent).next;

    }
    free((*pCurrent).strName);
    free((*pCurrent).strValue);
    free(pCurrent);
    dict->nCurrentSize--;
    break;
   }

   pPrev = pCurrent;
   pCurrent = (*pCurrent).next;
  }
 }
 else
 {
  //Should I have to intimate user??
 }

 return nReturnValue;
}


These functions will delete entire dictionary.

int DeleteDictionaryNodeArray(DictionaryNode **dArray, int nSizeOfArray)
{
 int nReturnValue = 0;
 int i = 0, j = 0;
 DictionaryNode *pCurrent = 0, *pHead = 0;

 for (i = 0; i < nSizeOfArray; i++)
 {
  if (dArray[i] != 0)
  {
   pHead = dArray[i];
   while (pHead != 0)
   {
    if ((*pHead).strName != 0)
    {
     free((*pHead).strName);
     (*pHead).strName = 0;
    }

    if ((*pHead).strValue != 0)
    {
     free((*pHead).strValue);
     (*pHead).strValue = 0;
    }

    pCurrent = (*pCurrent).next;
    free(pHead);
    pHead = pCurrent;

   }

   dArray[i] = 0;
  }
 }

 free(dArray);
 dArray = 0;

 return nReturnValue;
}


int DeleteDictionary(Dictionary *dict)
{
 int nReturnValue = 0;
 int i = 0, j = 0;
 DictionaryNode *pCurrent = 0, *pHead = 0;

 if (dict != 0)
 {
  if ((*dict).dictionaryArray != 0)
  {
   nReturnValue = DeleteDictionaryNodeArray((*dict).dictionaryArray, (*dict).nSizeOfDictionary);
   (*dict).dictionaryArray = 0;
  }

  (*dict).LoadFactor = 0;
  (*dict).nCurrentSize = 0;
  (*dict).nSizeOfDictionary = 0;

  free(dict);
  dict = 0;
 }

 return nReturnValue;
}

Given a key, get the corresponding value stored in dictionary. This is a very important function of dictionary.

DictionaryNode* GetNodeFromDictionary(Dictionary *dict, char *strKey)
{
 DictionaryNode *pNode = 0;

 pNode = dict->dictionaryArray[hash(dict->nSizeOfDictionary, strKey)];

 while (pNode != 0)
 {
  if (strcmp(pNode->strName, strKey) == 0)
  {
   break;
  }
  
  pNode = pNode->next;
 }

 return pNode;
}


char* GetValueFromDictionary(Dictionary *dict, char *strKey)
{
 char *strValue = 0;

 DictionaryNode *pNode = GetNodeFromDictionary(dict, strKey);
 if (pNode != 0)
 {
  strValue = pNode->strValue;
 }

 return strValue;
}


Complete code can be found at git - https://github.com/harsha-kadekar/BasicHttpServerClient
Code is present in file SupportingDataStructures.c and SupportingDataStructures.h files.